[Algorithm] Minimum Spanning Tree (Prim & Kruskal)
- Computer Science/Algorithm
- 2017. 10. 21. 23:24
Minimum Spanning Tree(MST) 문제는 그래프에서 모든 정점을 연결해주는 최소 간선의 집합 중 가중치의 합이 가장 작은 간선의 집합을 찾는 문제입니다.
MST를 구하는 방법은 크게 2가지가 있습니다. Prim algorithm과 Kruskal algorithm이죠.
Prim과 Kruskal의 기본적인 아이디어는 다음과 같습니다.
Prim algorithm은 각 정점을 방문하며 그 정점에 연결된 가장 가중치가 작은 간선들을 선택하여 MST를 구합니다.
Kruskal algorithm은 각 간선들을 탐색하여 가장 가중치가 작은 간선들을 택하면서 MST를 구합니다.
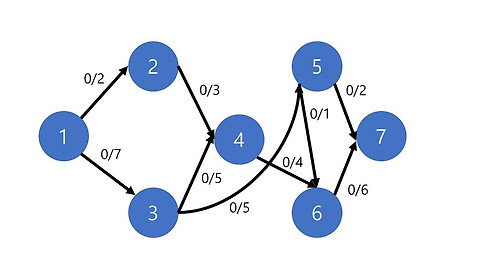
지금부터, 아래와 같은 그래프를 가지고 Prim algorithm과 Kruskal algorithm의 동작과정을 알아보고 각 알고리즘을 구현한 코드를 소개하도록 하겠습니다.
1) Prim algorithm
처음 시작하는 정점은 그래프에서 임의의 한 정점을 잡습니다. 여기서는 정점 1을 선택했습니다. 이 1에 연결된 간선들을 우선순위 큐에 삽입합니다. 그리고 간선 중 가장 가중치가 적은 간선 3을 선택하고 그와 연결된 정점 3을 MST의 요소로 추가합니다.
(초록색 간선으로 표시된 간선은 우선순위 큐에 들어있다는 표시이고, 오렌지색 간선은 MST의 요소에 포함되었다는 표시입니다.)
마찬가지로 정점 3에 연결된 간선들을 우선순위 큐에 추가합니다. 여기서 가장 가중치가 적은 간선인 1을 우선순위큐에서 꺼내어 MST에 추가합니다. 현재까지 MST에 추가된 간선은 가중치가 1,3인 간선입니다. 또한 우선순위 큐에는 4,6,7이 저장되지요. 선택된 정점은 {1,3}입니다. 이 연산을 마지막 정점이 선택될때까지 실행하면 MST가 완성됩니다.
MST의 구성 간선은 가중치를 기준으로 1,3,4,6,7 이 선택되었고 가중치의 총합은 21입니다.
1) Kruskal algorithm
Kruskal 알고리즘은 그래프의 모든 간선을 저장한 뒤 정렬합니다. 그리고 작은 간선부터 차례로 MST의 요소로서 추가합니다. 단, 추가할 시 간선을 이루는 두 정점이 같은 컴포넌트에 해당되면 안됩니다. 이를 확인하기 위해서 Disjoint-Set 자료형을 구현하여 같은 컴포넌트인지 아닌지를 판가름합니다.
MST를 이루는 간선은 가중치를 기준으로 {1,3,4,6,7} 입니다.
다음은 Prim과 Kruskal을 구현한 C++코드입니다.
Prim
#include <iostream>
#include <string>
#include <vector>
#include <algorithm>
#include <queue>
using namespace std;
#pragma warning(disable:4996)
const int INF = 987654321;
typedef struct Edge {
int s, t, w;
Edge(int _s, int _t, int _w) : s(_s), t(_t), w(_w) {}
};
vector<Edge> adj[100];
bool visited[100][100];
int main(void)
{
int N, M;
cin >> N >> M;
// 그래프 행렬 초기화
memset(visited, false, sizeof(visited));
for (int i = 0; i < 100; ++i)
adj[i].clear();
for (int m = 0, a, b, c; m < M; ++m) {
cin >> a >> b >> c;
if (a > b) swap(a, b);
adj[a].push_back(Edge(a, b, c));
adj[b].push_back(Edge(b, a, c));
}
auto comp = [](const Edge& a, const Edge& b) {
return a.w > b.w;
};
priority_queue<Edge, vector<Edge>, decltype(comp)> pq(comp);
int src = 1;
for (auto e : adj[src]) pq.push(e);
int cnt = 1;
int ret = 0;
while (!pq.empty()) {
Edge e = pq.top(); pq.pop();
if (visited[e.s][e.t]) continue;
visited[e.s][e.t] = visited[e.t][e.s] = true;
src = e.t;
for (auto e : adj[src]) pq.push(e);
ret += e.w;
cnt++;
if (cnt == N) break;
}
cout << ret << endl;
}
Kruskal
#include <iostream>
#include <string>
#include <vector>
#include <algorithm>
#include <queue>
#include <set>
using namespace std;
#pragma warning(disable:4996)
const int INF = 987654321;
typedef struct Edge {
int s, t, w;
Edge(int _s, int _t, int _w) : s(_s), t(_t), w(_w) {}
};
struct Disjoint {
int dis[100];
int rank[100];
Disjoint() {
memset(rank, 0, sizeof(rank));
for (int i = 0; i < 100; ++i)
dis[i] = i;
}
int find(int s) {
if (dis[s] == s) return s;
else return dis[s] = find(dis[s]);
}
void merge(int a, int b) {
a = find(a); b = find(b);
if (a == b) return;
if (rank[a] < rank[b]) {
dis[a] = b;
}
else if (rank[a] > rank[b]) {
dis[b] = a;
}
else {
dis[a] = b;
rank[b]++;
}
}
};
int main(void)
{
int N, M;
cin >> N >> M;
// 그래프 행렬 초기화
Disjoint disj;
auto comp = [](const Edge& a, const Edge& b) {
return a.w > b.w;
};
priority_queue< Edge, vector<Edge>, decltype(comp)> pq(comp);
for (int m = 0, a, b, c; m < M; ++m) {
cin >> a >> b >> c;
pq.push(Edge(a, b, c));
}
int cnt = 1;
int ret = 0;
while (!pq.empty()) {
Edge e = pq.top(); pq.pop();
if (disj.find(e.s) == disj.find(e.t)) continue;
ret += e.w;
cnt++;
if (cnt == N) break;
}
cout << ret << endl;
}
'Computer Science > Algorithm' 카테고리의 다른 글
| [Algorithm]Floyd-Warshall(플로이드-워샬 알고리즘) (0) | 2017.10.17 |
|---|---|
| [Algorithm] Bellman-Ford(벨만포드) (2) | 2017.10.09 |
| [Algorithm] LCS(Longest Common Subsequence) (0) | 2017.10.06 |
| [Algorithm] 네트워크 유량(Network Flow) (0) | 2017.10.01 |
| [Algorithm] 소수 구하기 (0) | 2017.04.15 |
이 글을 공유하기